Dynamic occupancy models in unmarked
Marc Kéry, Swiss Ornithological Institute
Richard Chandler, University of Georgia
August 16, 2016
Source:vignettes/colext.Rmd
colext.RmdAbstract
Dynamic occupancy models (MacKenzie et al. 2003) allow inference about the occurrence of “things” at collections of “sites” and about how changes in occurrence are driven by colonization and local extinction. These models also account for imperfect detection probability. Depending on how “thing” and “site” are defined, occupancy may have vastly different biological meanings, including the presence of a disease in an individual (disease incidence) of a species at a site (occurrence, distribution), or of an individual in a territory. Dynamic occupancy models in unmarked are fit using the function colext. All parameters can be modeled as functions of covariates, i.e., first-year occupancy with covariates varying by site (site-covariates), colonization and survival with site- and yearly-site-covariates and detection with site-, yearly-site- and sample-occasion-covariates. We give two commented example analyses: one for a simulated data set and another for a real data set on crossbills in the Swiss breeding bird survey MHB. We also give examples to show how predictions, along with standard errors and confidence intervals, can be obtained.
Introduction
Occurrence is a quantity of central importance in many branches of ecology and related sciences. The presence of a disease in an individual or of a species at a site are two common types of occurrence studies. The associated biological metrics are the incidence of the disease and species occurrence or species distribution. Thus, depending on how we define the thing we are looking for and the sample unit, very different biological quantities can be analyzed using statistical models for occupancy.
If we denote presence of the “thing” as \(y=1\) and its absence as \(y=0\), then it is natural to characterize all these metrics by the probability that a randomly chosen sample unit (“site”) is occupied, i.e., has a “thing” present: \(Pr(y=1) = \psi\). We call this the occupancy probability, or occupancy for short, and from now on will call the sample unit, where the presence or absence of a “thing” is assessed, generically a “site”.
Naturally, we would like to explore factors that affect the likelihood that a site is occupied. A binomial generalized linear model, or logistic regression, is the customary statistical model for occurrence. In this model, we treat occurrence \(y\) as a binomial random variable with trial size 1 and success probability \(p\), or, equivalently, a Bernoulli trial with \(p\). “Success” means occurrence, so \(p\) is the occurrence probability. It can be modeled as a linear or other function of covariates via a suitable link function, e.g., the logit link. This simple model is described in many places, including McCullagh and Nelder (1989), Royle and Dorazio (2008 chap. 3), Kéry (2010 chap. 17) and Kéry and Schaub (2011 chap. 3).
A generalization of this model accounts for changes in the occupancy state of sites by introducing parameters for survival (or alternatively, extinction) and colonization probability. Thus, when we have observations of occurrence for more than a single point in time, we can model the transition of the occupancy state at site \(i\) between successive times as another Bernoulli trial. To model the fate of an occupied site, we denote the probability that a site occupied at \(t\) is again occupied at \(t+1\) as \(Pr(y_{i,t+1} = 1 | y_{i,t} = 1 ) = \phi\). This represents the survival probability of a site that is occupied. Of course, we could also choose to express this component of occupancy dynamics by the converse, extinction probability \(\epsilon\) — the parameterization used in unmarked. To model the fate of an unoccupied site, we denote as \(Pr(y_{i,t+1} = 1 | y_{i,t} = 0 ) = \gamma\) the probability that an unoccupied site at \(t\) becomes occupied at \(t+1\). This is the colonization probability of an empty site. Such a dynamic model of occurrence has become famous in the ecological literature under the name “metapopulation model” (Hanski 1998).
However, when using ecological data collected in the field to fit such models of occurrence, we face the usual challenge of imperfect detection (e.g. Kéry and Schmidt 2008). For instance, a species can go unobserved at a surveyed site or an occupied territory can appear unoccupied during a particular survey, perhaps because both birds are away hunting. Not accounting for detection error may seriously bias all parameter estimators of a metapopulation model (Moilanen 2002, Royle and Dorazio 2008). To account for this additional stochastic component in the generation of most ecological field data, the classical metapopulation model may be generalized to include a submodel for the observation process, which allows an occupied site to be recorded as unoccupied. This model has been developed by MacKenzie et al. (2003). It is described as a hierarchical model by Royle (2007), Royle and Dorazio (2008 chap. 9) and Kéry and Schaub (2011 chap. 13). The model is usually called a multi-season, multi-year or a dynamic site-occupancy model. The former terms denote the fact that it is applied to multiple “seasons” or years and the latter emphasizes that the model allows for between-season occurrence dynamics.
This vignette describes the use of the unmarked function colext to fit dynamic occupancy models. Note that we will use italics for the names of functions. Static occupancy models, i.e., for a single season without changes in the occupancy state (MacKenzie et al. 2002), can be fit with occu, for the model described by MacKenzie et al. (2002) and Tyre et al. (2003), and with occuRN, for the heterogeneity occupancy model described by Royle and Nichols (2003). In the next section (section 2), we give a more technical description of the dynamic occupancy model. In section 3, we provide R code for generating data under a basic dynamic occupancy model and illustrate use of colext for fitting the model. In section 4, we use real data from the Swiss breeding bird survey MHB (Schmid et al. 2004) to fit a few more elaborate models with covariates for all parameters. We also give examples illustrating how to compute predictions, with standard errors and 95% confidence intervals, for the parameters.
Dynamic occupancy models
To be able to estimate the parameters of the dynamic occupancy model (probabilities of occurrence, survival and colonization) separately from the parameters for the observation process (detection probability), replicate observations are required from a period of closure, during which the occupancy state of a site must remain constant, i.e., it is either occupied or unoccupied. The modeled data \(y_{ijt}\) are indicators for whether a species is detected at site \(i\) (\(i = 1, 2, \ldots M\)), during replicate survey \(j\) (\(j = 1, 2, \ldots J\)) in season \(t\) (\(t = 1, 2, \ldots T\)). That is, \(y_{ijt}=1\) if at least one individual is detected and \(y_{ijt}=0\) if none is detected.
The model makes the following assumptions: * replicate surveys at a site during a single season are independent (or else dependency must be modeled) * occurrence state \(z_{it}\) (see below) does not change over replicate surveys at site \(i\) during season \(t\) * there are no false-positive errors, i.e., a species can only be overlooked where it occurs, but it cannot be detected where it does not in fact occur (i.e., there are no false-positives)
The complete model consists of one submodel to describe the ecological process, or state, and another submodel for the observation process, which is dependent on the result of the ecological process. The ecological process describes the latent occurrence dynamics for all sites in terms of parameters for the probability of initial occurrence and site survival and colonization. The observation process describes the probability of detecting a presence (i.e., \(y = 1\)) at a site that is occupied and takes account of false-negative observation errors.
Ecological or state process
This initial state is denoted \(z_{i1}\) and represents occurrence at site \(i\) during season 1. For this, the model assumes a Bernoulli trial governed by the occupancy probability in the first season \(\psi_{i1}\):
\[ z_{i1} = Bernoulli(\psi_{i1}) \]
We must distinguish the sample quantity “occurrence” at a site, \(z\), from the population quantity “occupancy probability”, \(\psi\). The former is the realization of a Bernoulli random variable with parameter \(\psi\). This distinction becomes important when we want to compute the number of occupied sites among the sample of surveyed sites; see Royle (2007) and Weir and Royle (2009) for this distinction.
For all later seasons (\(t = 2, 3, \ldots T\)), occurrence is a function of occurrence at site \(i\) at time \(t-1\) and one of two parameters that describe the colonization-extinction dynamics of the system. These dynamic parameters are the probability of local survival \(\phi_{it}\), also called probability of persistence (= 1 minus the probability of local extinction), and the probability of colonization \(\gamma_{it}\).
\[ z_{it} \sim Bernoulli(z_{i,t-1} \phi_{it} + (1-z_{i,t-1}) \gamma_{it}) \]
Hence, if site \(i\) is unoccupied at \(t-1\) , \(z_{i,t-1}=0\), and the success probability of the Bernoulli is \(0*\phi_{it} + (1-0) * \gamma_{it}\), so the site is occupied (=colonized) in season \(t\) with probability \(\gamma_{it}\) . Conversely, if site \(i\) is occupied at \(t-1\) , \(z_{i,t-1}=1\), and the success probability of the Bernoulli is given by \(1*\phi_{it} + (1-1) * \gamma_{it}\), so the site is occupied in (=survives to) season \(t\) with probability \(\phi_{it}\).
Occupancy probability (\(\psi_{it}\)) and occurrence (\(z_{it}\)) at all later times \(t\) can be computed recursively from \(\psi_{i1}\), \(z_{i1}\) , \(\phi_{it}\) and \(\gamma_{it}\). Variances of these derived estimates can be obtained via the delta method or the bootstrap.
Observation process
To account for the observation error (specifically, false-negative observations), the conventional Bernoulli detection process is assumed, such that
\[ y_{ijt} \sim Bernoulli(z_{it} p_{ijt}) \]
Here, \(y_{ijt}\) is the detection probability at site \(i\) during survey \(j\) and season \(t\). Detection is conditional on occurrence, and multiplying \(p_{ijt}\) with \(z_{it}\) ensures that occurrence can only be detected where in fact a species occurs, i.e. where \(z_{it}=1\).
Modeling of parameters
The preceding, fully general model description allows for site-(\(i\)) dependence of all parameters. In addition to that, survival and colonization probabilities may be season-(\(t\))dependent and detection probability season-(\(t\)) and survey-(\(j\)) dependent. All this complexity may be dropped, especially the dependence on sites. On the other hand, all parameters that are indexed in some way can be modeled, e.g., as functions of covariates that vary along the dimension denoted by an index. We will fit linear functions (on the logit link scale) of covariates into first-year occupancy, survival and colonization and into detection probability. That is, for probabilities of first-year occupancy, survival, colonization and detection, respectively, we will fit models of the form \(logit(\psi_{i1}) = \alpha + \beta x_i\), where \(x_i\) may be forest cover or elevation of site \(i\) , \(logit(\phi_{it}) = \alpha + \beta x_{it}\), where \(x_{it}\) may be tree mast at site \(i\) during season \(t\), \(logit(\gamma_{it}) = \alpha + \beta x_{it}\), for a similarly defined covariate \(x_{it}\), or \(logit(p_{ijt}) = \alpha + \beta x_{ijt}\) , where \(x_{ijt}\) is the Julian date of the survey \(j\) at site \(i\) in season \(t\).
We note that for first-year occupancy, only covariates that vary among sites (“site covariates”) can be fitted, while for survival and colonization, covariates that vary by site and by season (“yearly site covariates”) may be fitted as well. For detection, covariates of three formats may be fitted: “site-covariates”, “yearly-site-covariates” and “observation-covariates”, as they are called in unmarked.
Dynamic occupancy models for simulated data
We first generate a simple, simulated data set with specified, year-specific values for the parameters as well as design specifications, i.e., number of sites, years and surveys per year. Then, we show how to fit a dynamic occupancy model with year-dependence in the parameters for colonization, extinction and detection probability.
Simulating, formatting, and summarizing data
To simulate the data, we execute the following R code. The actual values for these parameters for each year are drawn randomly from a uniform distribution with the specified bounds.
M <- 250 # Number of sites J <- 3 # num secondary sample periods T <- 10 # num primary sample periods psi <- rep(NA, T) # Occupancy probability muZ <- z <- array(dim = c(M, T)) # Expected and realized occurrence y <- array(NA, dim = c(M, J, T)) # Detection histories set.seed(13973) psi[1] <- 0.4 # Initial occupancy probability p <- c(0.3,0.4,0.5,0.5,0.1,0.3,0.5,0.5,0.6,0.2) phi <- runif(n=T-1, min=0.6, max=0.8) # Survival probability (1-epsilon) gamma <- runif(n=T-1, min=0.1, max=0.2) # Colonization probability # Generate latent states of occurrence # First year z[,1] <- rbinom(M, 1, psi[1]) # Initial occupancy state # Later years for(i in 1:M){ # Loop over sites for(k in 2:T){ # Loop over years muZ[k] <- z[i, k-1]*phi[k-1] + (1-z[i, k-1])*gamma[k-1] z[i,k] <- rbinom(1, 1, muZ[k]) } } # Generate detection/non-detection data for(i in 1:M){ for(k in 1:T){ prob <- z[i,k] * p[k] for(j in 1:J){ y[i,j,k] <- rbinom(1, 1, prob) } } } # Compute annual population occupancy for (k in 2:T){ psi[k] <- psi[k-1]*phi[k-1] + (1-psi[k-1])*gamma[k-1] }
We have now generated a single realization from the stochastic system thus defined. Figure 1 illustrates the fundamental issue of imperfect detection — the actual proportion of sites occupied differs greatly from the observed proportion of sites occupied, and because \(p\) varies among years, the observed data cannot be used as a valid index of the parameter of interest \(\psi_i\).
plot(1:T, colMeans(z), type = "b", xlab = "Year", ylab = "Proportion of sites occupied", col = "black", xlim=c(0.5, 10.5), xaxp=c(1,10,9), ylim = c(0,0.6), lwd = 2, lty = 1, frame.plot = FALSE, las = 1, pch=16) psi.app <- colMeans(apply(y, c(1,3), max)) lines(1:T, psi.app, type = "b", col = "blue", lty=3, lwd = 2) legend(1, 0.6, c("truth", "observed"), col=c("black", "blue"), lty=c(1,3), pch=c(16,1))
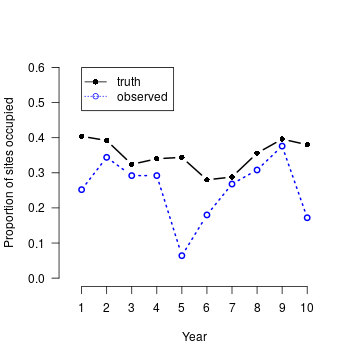
Figure 1. Summary of the multi-year occupancy data set generated.
To analyze this data set with a dynamic occupancy model in unmarked, we first load the package.
Next, we reformat the detection/non-detection data from a 3-dimensional array (as generated) into a 2-dimensional matrix with M rows. That is, we put the annual tables of data (the slices of the former 3-D array) sideways to produce a “wide” layout of the data.
yy <- matrix(y, M, J*T)
Next, we create a matrix indicating the year each site was surveyed.
To organize the data in the format required by colext, we make use of the function unmarkedMultFrame. The only required arguments are y, the detection/non-detection data, and numPrimary, the number of seasons. The three types of covariates described earlier can also be supplied using the arguments siteCovs, yearlySiteCovs, and obsCovs. In this case, we only make use of the second type, which must have M rows and T columns.
simUMF <- unmarkedMultFrame( y = yy, yearlySiteCovs = list(year = year), numPrimary=T) summary(simUMF)
## unmarkedFrame Object
##
## 250 sites
## Maximum number of observations per site: 30
## Mean number of observations per site: 30
## Number of primary survey periods: 10
## Number of secondary survey periods: 3
## Sites with at least one detection: 195
##
## Tabulation of y observations:
## 0 1
## 6430 1070
##
## Yearly-site-level covariates:
## year
## 01 : 250
## 02 : 250
## 03 : 250
## 04 : 250
## 05 : 250
## 06 : 250
## (Other):1000Model fitting
We are ready to fit a few dynamic occupancy models. We will fit a model with constant values for all parameters and another with full time-dependence for colonization, extinction and detection probability. We also time the calculations.
# Model with all constant parameters m0 <- colext(psiformula= ~1, gammaformula = ~ 1, epsilonformula = ~ 1, pformula = ~ 1, data = simUMF, method="BFGS") summary(m0)
##
## Call:
## colext(psiformula = ~1, gammaformula = ~1, epsilonformula = ~1,
## pformula = ~1, data = simUMF, method = "BFGS")
##
## Initial (logit-scale):
## Estimate SE z P(>|z|)
## -0.813 0.158 -5.16 2.46e-07
##
## Colonization (logit-scale):
## Estimate SE z P(>|z|)
## -1.77 0.0807 -22 2.75e-107
##
## Extinction (logit-scale):
## Estimate SE z P(>|z|)
## -0.59 0.102 -5.79 7.04e-09
##
## Detection (logit-scale):
## Estimate SE z P(>|z|)
## -0.0837 0.0562 -1.49 0.137
##
## AIC: 4972.597
## Number of sites: 250
## optim convergence code: 0
## optim iterations: 27
## Bootstrap iterations: 0The computation time was only a few seconds. Note that all parameters were estimated on the logit scale. To back-transform to the original scale, we can simply use the inverse-logit function, named plogis in R.
plogis(-0.813)
## [1] 0.3072516Alternatively, we can use backTransform, which computes standard errors using the delta method. Confidence intervals are also easily obtained using the function confint. We first remind ourselves of the names of parameters, which can all be used as arguments for these functions.
names(m0)
## [1] "psi" "col" "ext" "det"backTransform(m0, type="psi")
## Backtransformed linear combination(s) of Initial estimate(s)
##
## Estimate SE LinComb (Intercept)
## 0.307 0.0335 -0.813 1
##
## Transformation: logisticconfint(backTransform(m0, type="psi"))
## 0.025 0.975
## 0.2457313 0.3765804Next, we fit the dynamic occupancy model with full year-dependence in the parameters describing occupancy dynamics and also in detection. This is the same model under which we generated the data set, so we would expect accurate estimates.
By default in R, a factor such as year in this analysis, is a parameterized in terms of an intercept and effects representing differences. This would mean that the parameter for the first year is the intercept and the effects would denote the differences between the parameter values in all other years, relative to the parameter value in the first year, which serves as a reference level. This treatment or effects parameterization is useful for testing for differences. For simple presentation, a means parameterization is more practical. It can be specified by adding a -1 to the formula for the time-dependent parameters.
m1 <- colext(psiformula = ~1, # First-year occupancy gammaformula = ~ year-1, # Colonization epsilonformula = ~ year-1, # Extinction pformula = ~ year-1, # Detection data = simUMF) m1
##
## Call:
## colext(psiformula = ~1, gammaformula = ~year - 1, epsilonformula = ~year -
## 1, pformula = ~year - 1, data = simUMF)
##
## Initial:
## Estimate SE z P(>|z|)
## -0.273 0.302 -0.906 0.365
##
## Colonization:
## Estimate SE z P(>|z|)
## year01 -2.08 0.951 -2.19 2.86e-02
## year02 -2.18 0.365 -5.96 2.52e-09
## year03 -1.98 0.274 -7.23 4.88e-13
## year04 -2.32 0.678 -3.42 6.37e-04
## year05 -1.89 0.478 -3.95 7.78e-05
## year06 -1.76 0.294 -5.97 2.44e-09
## year07 -1.55 0.230 -6.73 1.75e-11
## year08 -1.43 0.228 -6.29 3.19e-10
## year09 -2.35 0.470 -5.00 5.64e-07
##
## Extinction:
## Estimate SE z P(>|z|)
## year01 -1.4209 0.418 -3.401 6.72e-04
## year02 -0.4808 0.239 -2.009 4.45e-02
## year03 -1.2606 0.366 -3.440 5.83e-04
## year04 -0.0907 0.650 -0.139 8.89e-01
## year05 -0.6456 0.599 -1.078 2.81e-01
## year06 -0.9586 0.378 -2.539 1.11e-02
## year07 -1.2279 0.365 -3.362 7.74e-04
## year08 -1.1894 0.292 -4.076 4.58e-05
## year09 -0.6292 0.635 -0.991 3.22e-01
##
## Detection:
## Estimate SE z P(>|z|)
## year01 -1.0824 0.244 -4.434 9.26e-06
## year02 -0.2232 0.148 -1.508 1.32e-01
## year03 0.2951 0.154 1.918 5.52e-02
## year04 0.0662 0.161 0.412 6.81e-01
## year05 -2.0396 0.433 -4.706 2.52e-06
## year06 -0.6982 0.232 -3.005 2.66e-03
## year07 0.2413 0.165 1.466 1.43e-01
## year08 0.0847 0.155 0.548 5.84e-01
## year09 0.6052 0.140 4.338 1.44e-05
## year10 -1.1699 0.306 -3.828 1.29e-04
##
## AIC: 4779.172Manipulating results: prediction and plotting
Again, all estimates are shown on the logit-scale. Back-transforming estimates when covariates, such as year, are present involves an extra step. Specifically, we need to tell unmarked the values of our covariate at which we want an estimate. This can be done using backTransform in combination with linearComb, although it can be easier to use predict. predict allows the user to supply a data.frame in which each row represents a combination of covariate values of interest. Below, we create data.frames called nd with each row representing a year. Then we request yearly estimates of the probability of extinction, colonization and detection, and compare them to “truth”, i.e., the values with which we simulated the data set. Note that there are T-1 extinction and colonization parameters in this case, so we do not need to include year 10 in nd.
nd <- data.frame(year=c('01','02','03','04','05','06','07','08','09')) E.ext <- predict(m1, type='ext', newdata=nd) E.col <- predict(m1, type='col', newdata=nd) nd <- data.frame(year=c('01','02','03','04','05','06','07','08','09','10')) E.det <- predict(m1, type='det', newdata=nd)
predict returns the predictions along with standard errors and confidence intervals. These can be used to create plots. The with function is used to simplify the process of requesting the columns of data.frame returned by predict.
op <- par(mfrow=c(3,1), mai=c(0.6, 0.6, 0.1, 0.1)) with(E.ext, { # Plot for extinction probability plot(1:9, Predicted, pch=1, xaxt='n', xlab='Year', ylab=expression(paste('Extinction probability ( ', epsilon, ' )')), ylim=c(0,1), col=4) axis(1, at=1:9, labels=nd$year[1:9]) arrows(1:9, lower, 1:9, upper, code=3, angle=90, length=0.03, col=4) points((1:9)-0.1, 1-phi, col=1, lwd = 1, pch=16) legend(7, 1, c('Parameter', 'Estimate'), col=c(1,4), pch=c(16, 1), cex=0.8) }) with(E.col, { # Plot for colonization probability plot(1:9, Predicted, pch=1, xaxt='n', xlab='Year', ylab=expression(paste('Colonization probability ( ', gamma, ' )')), ylim=c(0,1), col=4) axis(1, at=1:9, labels=nd$year[1:9]) arrows(1:9, lower, 1:9, upper, code=3, angle=90, length=0.03, col=4) points((1:9)-0.1, gamma, col=1, lwd = 1, pch=16) legend(7, 1, c('Parameter', 'Estimate'), col=c(1,4), pch=c(16, 1), cex=0.8) }) with(E.det, { # Plot for detection probability: note 10 years plot(1:10, Predicted, pch=1, xaxt='n', xlab='Year', ylab=expression(paste('Detection probability ( ', p, ' )')), ylim=c(0,1), col=4) axis(1, at=1:10, labels=nd$year) arrows(1:10, lower, 1:10, upper, code=3, angle=90, length=0.03, col=4) points((1:10)-0.1, p, col=1, lwd = 1, pch=16) legend(7.5, 1, c('Parameter','Estimate'), col=c(1,4), pch=c(16, 1), cex=0.8) })
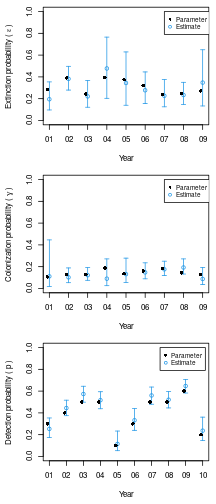
Figure 2. Yearly estimates of parameters
par(op)
Figure 2 shows that the 95% confidence intervals include the true parameter values, and the point estimates are not too far off.
Derived parameters
Estimates of occupancy probability in years \(T>1\) must be derived from the estimates of first-year occupancy and the two parameters governing the dynamics, extinction/survival and colonization. unmarked does this automatically in two ways. First, the population-level estimates of occupancy probability \(\psi_t = \psi_{t-1}\phi_{t-1} + (1-\phi_{t-1})\gamma\) are calculated and stored in the slot named . Slots can be accessed using the @ operator, e.g. fm@projected. In some cases, interest may lie in making inference about the proportion of the sampled sites that are occupied, rather than the entire population of sites. These estimates are contained in the smoothed slot of the fitted model. Thus, the projected values are estimates of population parameters, and the smoothed estimates are of the finite-sample quantities. Discussions of the differences can be found in Weir and Royle (2009).
Bootstrap methods can be used to compute standard errors of derived parameter estimates. Here we employ a non-parametric bootstrap to obtain standard errors of the smoothed estimates of occupancy probability during each year.
m1 <- nonparboot(m1, B = 10) cbind(psi=psi, smoothed=smoothed(m1)[2,], SE=m1@smoothed.mean.bsse[2,])
## psi smoothed SE
## 1 0.4000000 0.4320671 0.06783911
## 2 0.3493746 0.4110124 0.03786402
## 3 0.2977125 0.3139967 0.02780818
## 4 0.3148447 0.3278179 0.04303542
## 5 0.3192990 0.2316695 0.10858419
## 6 0.2915934 0.2528485 0.04179036
## 7 0.3114415 0.2928429 0.03113920
## 8 0.3636580 0.3504885 0.04224678
## 9 0.3654064 0.3936991 0.02103870
## 10 0.3460641 0.3095786 0.06830698In practice, B should be much higher, possibly >1000 for complex models .
Another derived parameters of interest is turnover probability
\[ \tau_t = \frac{\gamma_{t-1}(1-\psi_{t-1})}{\gamma_{t-1}(1-\psi_{t-1}) + \phi_{t-1}\psi_{t-1}} \]
The following function returns these estimates.
turnover <- function(fm) { psi.hat <- plogis(coef(fm, type="psi")) if(length(psi.hat) > 1) stop("this function only works if psi is scalar") T <- getData(fm)@numPrimary tau.hat <- numeric(T-1) gamma.hat <- plogis(coef(fm, type="col")) phi.hat <- 1 - plogis(coef(fm, type="ext")) if(length(gamma.hat) != T-1 | length(phi.hat) != T-1) stop("this function only works if gamma and phi T-1 vectors") for(t in 2:T) { psi.hat[t] <- psi.hat[t-1]*phi.hat[t-1] + (1-psi.hat[t-1])*gamma.hat[t-1] tau.hat[t-1] <- gamma.hat[t-1]*(1-psi.hat[t-1]) / psi.hat[t] } return(tau.hat) }
The bootstrap again offers a means of estimating variance. Here we show how to generate 95% confidence intervals for the turnover estimates using the parametric bootstrap.
pb <- parboot(m1, statistic=turnover, nsim=2) turnCI <- cbind(pb@t0, t(apply(pb@t.star, 2, quantile, probs=c(0.025, 0.975)))) colnames(turnCI) <- c("tau", "lower", "upper") turnCI
## tau lower upper
## t*1 0.1532645 0.00536045 0.1974714
## t*2 0.1911530 0.07881180 0.2119585
## t*3 0.2537292 0.19777204 0.2785973
## t*4 0.2604356 0.04063769 0.4197328
## t*5 0.3989303 0.34078483 0.4720357
## t*6 0.3758690 0.32703698 0.5370796
## t*7 0.3537473 0.32696166 0.3564059
## t*8 0.3174983 0.32925238 0.4139696
## t*9 0.1704449 0.18946470 0.3186236Which bootstrap method is most appropriate for variance estimation? For detailed distinctions between the non-parametric and the parametric bootstrap, see Davison and Hinkley (1997). We note simply that the parametric bootstrap resamples from the fitted model, and thus the measures of uncertainty are purely functions of the distributions assumed by the model. Non-parametric bootstrap samples, in contrast, are obtained by resampling the data, not the model, and thus are not necessarily affected by the variance formulas of the model’s distributions.
Goodness-of-fit
In addition to estimating the variance of an estimate, the parametric bootstrap can be used to assess goodness-of-fit. For this purpose, a fit-statistic, i.e. one that compares observed and expected values, is evaluated using the original fitted model, and numerous other models fitted to simulated datasets. The simulation yields an approximation of the distribution of the fit-statistic, and a -value can be computed as the proportion of simulated values greater than the observed value.
Hosmer et al. (1997) found that a \(\chi^2\) statistic performed reasonably well in assessing lack of fit for logistic regression models. We know of no studies formally evaluating the performance of various fit-statistics for dynamic occupancy models, so this approach should be considered experimental. Fit-statistics applied to aggregated encounter histories offer an alternative approach (MacKenzie and Bailey 2004), but are difficult to implement when J*T is high and missing values or continuous covariates are present.
chisq <- function(fm) { umf <- getData(fm) y <- getY(umf) sr <- fm@sitesRemoved if(length(sr)>0) y <- y[-sr,,drop=FALSE] fv <- fitted(fm, na.rm=TRUE) y[is.na(fv)] <- NA sum((y-fv)^2/(fv*(1-fv))) } set.seed(344) pb.gof <- parboot(m0, statistic=chisq, nsim=100) plot(pb.gof, xlab=expression(chi^2), main="", col=gray(0.95), xlim=c(7300, 7700))
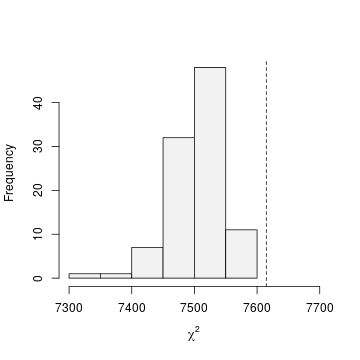
Figure 3. Goodness-of-fit
Figure 3 indicates that, as expected, the constant parameter model does not fit the data well.
Dynamic occupancy models for crossbill data from the Swiss MHB
The crossbill data set
The crossbill data are included with the unmarked package. The dataset contains the results of nine years of surveys (1999–2007) for the European crossbill (Loxia curvirostra), a pine-seed eating finch, in 267 1-km\(^2\) sample quadrats in Switzerland. Quadrats are surveyed annually as part of the Swiss breeding bird survey MHB (Schmid et al. 2004). They are laid out as a grid over Switzerland and surveyed 2 or 3 times every breeding season (mid-April to late June) by experienced field ornithologists along a haphazard survey route of length 1-9 km (average 5 km). High-elevation sites are only surveyed twice per breeding season.
Importing, formatting, and summarizing data
The data can be loaded into an open R workspace using the data command.
## [1] "id" "ele" "forest" "surveys" "det991" "det992" "det993"
## [8] "det001" "det002" "det003" "det011" "det012" "det013" "det021"
## [15] "det022" "det023" "det031" "det032" "det033" "det041" "det042"
## [22] "det043" "det051" "det052" "det053" "det061" "det062" "det063"
## [29] "det071" "det072" "det073" "date991" "date992" "date993" "date001"
## [36] "date002" "date003" "date011" "date012" "date013" "date021" "date022"
## [43] "date023" "date031" "date032" "date033" "date041" "date042" "date043"
## [50] "date051" "date052" "date053" "date061" "date062" "date063" "date071"
## [57] "date072" "date073"We have three covariates that vary by site: median elevation of the quadrat (ele, in metres), forest cover of the quadrat (forest, in percent) and the number of surveys per season (i.e., 2 or 3, surveys). These are called site covariates, because they vary by sites only. The 27 columns entitled det991 - det073 contain the crossbill detection/nondetection data during all surveys over the 9 years. They contain a 1 when at least one crossbill was recorded during a survey and a 0 otherwise. NAs indicate surveys that did not take place, either because a site is high-elevation and has no third survey or because it failed to be surveyed altogether in a year. The final 27 columns entitled date991 - date073 give the Julian date of each survey. They represent a “survey-covariate” or “observation covariate”. We note that the paper by Royle (2007) used a subset of this data set.
AIC-based model selection (see section 5.4) requires that all models are fit to the same data. unmarked removes missing data in a context specific way. For missing siteCovs, the entire row of data must be removed. However, for missing yearlySiteCovs or obsCovs, only the corresponding observation are removed. Thus, if unmarked removes different observations from different models, the models cannot be compared using AIC. A way around this is to remove the detection data corresponding to missing covariates before fitting the models. The crossbill data have missing dates and so we remove the associated detection/non-detection data.
DATE <- as.matrix(crossbill[,32:58]) y.cross <- as.matrix(crossbill[,5:31]) y.cross[is.na(DATE) != is.na(y.cross)] <- NA
In addition, continuous covariates should be transformed in a way that brings their values close to zero in order to improve or even enable numerical convergence of the maximum-likelihood routine. We do this “by hand” and note that we could also have used the R function scale. We subtract the mean and divide by the standard deviation.
sd.DATE <- sd(c(DATE), na.rm=TRUE) mean.DATE <- mean(DATE, na.rm=TRUE) DATE <- (DATE - mean.DATE) / sd.DATE
Before we can fit occupancy models, we need to format this data set appropriately.
years <- as.character(1999:2007) years <- matrix(years, nrow(crossbill), 9, byrow=TRUE) umf <- unmarkedMultFrame(y=y.cross, siteCovs=crossbill[,2:3], yearlySiteCovs=list(year=years), obsCovs=list(date=DATE), numPrimary=9)
Model fitting
We fit a series of models that represent different hypotheses about the colonization-extinction dynamics of Swiss crossbills at a spatial scale of 1 km\(^2\). We fit year effects on colonization and extinction in the means parameterization, but for detection probability, we choose an effects parameterization. The latter is more useful for getting predictions in the presence of other explanatory variables for that parameter. For model fm5 with more complex covariate relationships, we use as starting values for the optimization routine the solution from a “neighboring” model with slightly less complexity, model fm4. Wise choice of starting values can be decisive for success or failure of maximum likelihood estimation.
# A model with constant parameters fm0 <- colext(~1, ~1, ~1, ~1, umf) # Like fm0, but with year-dependent detection fm1 <- colext(~1, ~1, ~1, ~year, umf) # Like fm0, but with year-dependent colonization and extinction fm2 <- colext(~1, ~year-1, ~year-1, ~1, umf) # A fully time-dependent model fm3 <- colext(~1, ~year-1, ~year-1, ~year, umf) # Like fm3 with forest-dependence of 1st-year occupancy fm4 <- colext(~forest, ~year-1, ~year-1, ~year, umf) # Like fm4 with date- and year-dependence of detection fm5 <- colext(~forest, ~year-1, ~year-1, ~year + date + I(date^2), umf, starts=c(coef(fm4), 0, 0)) # Same as fm5, but with detection in addition depending on forest cover fm6 <- colext(~forest, ~year-1, ~year-1, ~year + date + I(date^2) + forest, umf)
Model selection
We can compare models using the Akaike information criterion (\(AIC\)). Note that unmarked yields \(AIC\), not \(AIC_c\) because the latter would require the sample size, which is not really known for hierarchical models such as the dynamic occupancy model.
Model selection and model-averaged prediction in unmarked require that we create a list of models using fitList. This function organizes models and conducts a series of tests to ensure that the models were fit to the same data.
models <- fitList('psi(.)gam(.)eps(.)p(.)' = fm0, 'psi(.)gam(.)eps(.)p(Y)' = fm1, 'psi(.)gam(Y)eps(Y)p(.)' = fm2, 'psi(.)gam(Y)eps(Y)p(Y)' = fm3, 'psi(F)gam(Y)eps(Y)p(Y)' = fm4, 'psi(F)gam(Y)eps(Y)p(YD2)' = fm5, 'psi(F)gam(Y)eps(Y)p(YD2F)' = fm6) ms <- modSel(models) ms
## nPars AIC delta AICwt cumltvWt
## psi(F)gam(Y)eps(Y)p(YD2F) 30 4986.39 0.00 1.0e+00 1.00
## psi(F)gam(Y)eps(Y)p(YD2) 29 5059.30 72.91 1.5e-16 1.00
## psi(F)gam(Y)eps(Y)p(Y) 27 5095.38 108.99 2.2e-24 1.00
## psi(.)gam(.)eps(.)p(Y) 12 5111.32 124.93 7.5e-28 1.00
## psi(.)gam(Y)eps(Y)p(Y) 26 5127.63 141.24 2.1e-31 1.00
## psi(.)gam(Y)eps(Y)p(.) 18 5170.54 184.15 1.0e-40 1.00
## psi(.)gam(.)eps(.)p(.) 4 5193.50 207.11 1.1e-45 1.00One model has overwhelming support, so we can base inference on that one alone. Before doing so, we point out how to extract coefficients from a fitList object, and convert the results to a data.frame, which could be exported from R.
Manipulating results: Prediction and plotting
Fitted models can be used to predict expected outcomes when given new data. For example, one could ask “how many crossbills would you expect to find in a quadrat with 50% forest cover?” Prediction also offers a way of presenting the results of an analysis. We illustrate by plotting the predictions of \(\psi\) and \(p\) over the range of covariate values studied. Note that because we standardized date, we need to transform it back to its original scale after obtaining predictions on the standardized scale.
op <- par(mfrow=c(1,2), mai=c(0.8,0.8,0.1,0.1)) nd <- data.frame(forest=seq(0, 100, length=50)) E.psi <- predict(fm6, type="psi", newdata=nd, appendData=TRUE) with(E.psi, { plot(forest, Predicted, ylim=c(0,1), type="l", xlab="Percent cover of forest", ylab=expression(hat(psi)), cex.lab=0.8, cex.axis=0.8) lines(forest, Predicted+1.96*SE, col=gray(0.7)) lines(forest, Predicted-1.96*SE, col=gray(0.7)) }) nd <- data.frame(date=seq(-2, 2, length=50), year=factor("2005", levels=c(unique(years))), forest=50) E.p <- predict(fm6, type="det", newdata=nd, appendData=TRUE) E.p$dateOrig <- E.p$date*sd.DATE + mean.DATE with(E.p, { plot(dateOrig, Predicted, ylim=c(0,1), type="l", xlab="Julian date", ylab=expression( italic(p) ), cex.lab=0.8, cex.axis=0.8) lines(dateOrig, Predicted+1.96*SE, col=gray(0.7)) lines(dateOrig, Predicted-1.96*SE, col=gray(0.7)) })
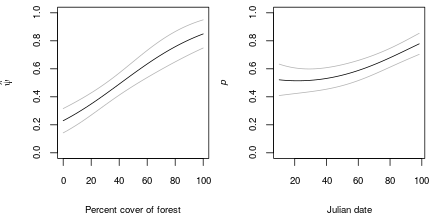
Figure 4. Covariates
par(op)
Acknowledgments
Special thanks goes to Ian Fiske, the author of colext and the original developer of unmarked. Andy Royle provided the initial funding and support for the package. The questions of many people on the users’ list motivated the writing of this document.
References
Davison, A. C., and D. V. Hinkley. 1997. Bootstrap methods and their application. Cambridge University Press.
Hanski, I. 1998. Metapopulation dynamics. Nature 396:41–49.
Hosmer, D. W., T. Hosmer, S. le Cressie, and S. Lemeshow. 1997. A comparision of goodness-of-fit tests for the logistic regression model. Statistics in Medicine 16:965–980.
Kéry, M. 2010. Introduction to WinBUGS for Ecologists. Academic Press.
Kéry, M., and M. Schaub. 2011. Bayesian Population Analysis using WinBUGS: A Hierarchical Perspective. Academic Press.
Kéry, M., and B. R. Schmidt. 2008. Imperfect detection and its consequences for monitoring for conservation. Community Ecology 9:207–2016.
MacKenzie, D. I., and L. Bailey. 2004. Assessing the fit of site-occupancy models. Journal of Agricultural, Biological, and Environmental Statistics 9:300–318.
MacKenzie, D. I., J. D. Nichols, J. E. Hines, M. G. Knutson, and A. B. Franklin. 2003. Estimating site occupancy, colonization, and local extinction when a species is detected imperfectly. Ecology 84:2200–2207.
MacKenzie, D. I., J. D. Nichols, G. B. Lachman, S. Droege, J. A. Royle, and C. A. Langtimm. 2002. Estimating site occupancy rates when detection probabilities are less than one. Ecology 83:2248–2255.
McCullagh, P., and J. A. Nelder. 1989. Generalized linear models. Chapman; Hall.
Moilanen, A. 2002. Implications of empirical data quality to metapopulation model parameter estimation and application. Oikos 96:516–530.
Royle, and K., J. A. 2007. A Bayesian state-space formulation of dynamic occupancy models. Ecology 88:1813–1823.
Royle, J. A., and R. M. Dorazio. 2008. Hierarchical modeling and inference in ecology: The analysis of data from populations, metapopulations and communities. Academic Press.
Royle, J. A., and J. D. Nichols. 2003. Estimating abundance from repeated presence-absence data or point counts. Ecology 84:777–790.
Schmid, H., N. Zbinden, and V. Keller. 2004. Überwachung der bestandsentwicklung häufiger brutvögel in der schweiz. Swiss Ornithological Institute Sempach Switzerland.
Tyre, A. J., B. Tenhumberg, S. A. Field, D. Niejalke, Parris K., and H. P. Possingham. 2003. Improving precision and reducing bias in biological surveys: Estimating false-negative error rates. Ecological Applications 13:1790–1801.
Weir, I. J. F., L., and J. A. Royle. 2009. Trends in anuran occupancy from northeastern states of the North American Amphibian Monitoring Program. Herpetological Conservation and Biology 4:389–402.