Distance sampling analysis in unmarked

Richard Chandler, USGS Patuxent Wildlife Research Center

March 4, 2020

Abstract

Distance sampling is a wildlife sampling technique used to estimate population size or density. Describing how density varies spatially is often of equal interest; however, conventional methods of analysis do not allow for explicit modeling of both density and detection probability. The function distsamp implements the multinomial-Poisson mixture model of Royle et al. (2004), which was developed to overcome this limitation. This model requires that line- or point-transects are spatially replicated and that distance data are recorded in discrete intervals. The function extends this basic model, by introducing the parameter \(\phi\), the probability of being available for detection (Chandler et al. 2011). Furthermore, this function allows abundance to be modeled using the negative binomial distribution, which may be useful for dealing with over-dispersion. This document describes how to format data, fit models, and manipulate results in package . It does not cover the statistical theory and assumptions underlying distance sampling (Buckland et al. 2001), which the user is expected to be familiar with.

Introduction

Spatial variation in density is common to virtually all wildlife populations, and describing this variation is a central objective of much research. To accurately estimate and model density, it is often necessary to account for individuals present but not detected. Distance from observer is a ubiquitous source of variation in detection probability, and thus distance sampling has become a commonly used survey methodology. Numerous options exist for analyzing distance sampling data, but here the focus is on the model of Royle et al. (2004), which assumes that multiple transects have been surveyed and distance data are recorded in discrete intervals. The details of the model formulation are as follows:

The latent transect-level abundance distribution is currently assumed to be \[ \label{eq:1} N_{i} \sim \mathrm{Poisson}(\lambda) \quad i=1,\dots,M\ \] The detection process is modeled as \[ \label{eq:2} y_{ij} \sim \mathrm{Multinomial}(N_{i}, \pi_{ij}) \quad i=1,\dots,M\;j=1,\dots,J \] where \(\pi_{ij}\) is the multinomial cell probability for transect \(i\) in distance class \(j\). These are computed by integrating a detection function such as the half-normal (with scale parameter \(\sigma\)) over each distance interval.

Parameters \(\lambda\) and \(\sigma\) can be vectors affected by transect-specific covariates using the log link.

Importing, formatting, and summarizing data

The first step is to import the data into R. The simplest option is to use the read.csv function to import a .csv file that has been formatted so that each row represents a transect, and columns describe either the number of individuals detected in each distance interval or transect-specific covariates. Alternatively, if data were not recorded in discrete distance intervals, a .csv file could be imported that contains a row for each individual detected and columns for the distances and transect names. This could then be converted to transect-level data using the function formatDistData. For example,

library(unmarked)
dists <- read.csv(system.file("csv", "distdata.csv", package="unmarked"),
                  stringsAsFactors=TRUE)
head(dists, 10)

##    distance transect
## 1         1        a
## 2        18        a
## 3         7        a
## 4         2        a
## 5        13        b
## 6         3        b
## 7         5        b
## 8        10        b
## 9         6        c
## 10        9        c

levels(dists$transect) <- c(levels(dists$transect), "g")
levels(dists$transect)

## [1] "a" "b" "c" "d" "e" "f" "g"

yDat <- formatDistData(dists, distCol="distance",
    transectNameCol="transect", dist.breaks=c(0, 5, 10, 15, 20))
yDat

##   [0,5] (5,10] (10,15] (15,20]
## a     2      1       0       1
## b     2      1       1       0
## c     2      2       0       0
## d     2      1       1       0
## e     1      0       1       2
## f     2      1       1       0
## g     0      0       0       0

Here we have created an object called yDat that contains counts for each transect (row) in each distance interval (columns). Note the method used to include transect "g", which was surveyed but where no individuals were detected. It is important that all surveyed transects are included in the analysis.

Suppose there also exists transect-specific covariate data.

(covs <- data.frame(canopyHt = c(5, 8, 3, 2, 4, 7, 5),
    habitat = c('A','A','A','A','B','B','B'), row.names=letters[1:7]))

##   canopyHt habitat
## a        5       A
## b        8       A
## c        3       A
## d        2       A
## e        4       B
## f        7       B
## g        5       B

The function unmarkedFrameDS can now be used to organize these data along with their metadata (study design (line- or point-transect), distance class break points, transect lengths, and units of measurement) into an object to be used as the data argument in distsamp. By organizing the data this way, the user does not need to repetitively specify these arguments during each call to distsamp, thereby reducing the potential for errors and facilitating data summary and manipulation.

umf <- unmarkedFrameDS(y=as.matrix(yDat), siteCovs=covs, survey="line",
    dist.breaks=c(0, 5, 10, 15, 20), tlength=rep(100, 7),
    unitsIn="m")

## Warning: siteCovs contains characters. Converting them to factors.

Note that there is no obsCovs argument, meaning that distance-interval-level covariates cannot be included in the analysis. The call to unmarkedFrameDS indicates that the data were collected on seven line transects, each 100 meters long, and detections were tabulated into distance intervals defined by the dist.breaks cutpoints. It is important that both transect lengths and distance break points are provided in the same units specified by unitsIn.

We can look at these data using a variety of methods.

summary(umf)

## unmarkedFrameDS Object
## 
## line-transect survey design
## Distance class cutpoints (m):  0 5 10 15 20 
## 
## 7 sites
## Maximum number of distance classes per site: 4 
## Mean number of distance classes per site: 4 
## Sites with at least one detection: 6 
## 
## Tabulation of y observations:
##  0  1  2 
## 11 10  7 
## 
## Site-level covariates:
##     canopyHt     habitat
##  Min.   :2.000   A:4    
##  1st Qu.:3.500   B:3    
##  Median :5.000          
##  Mean   :4.857          
##  3rd Qu.:6.000          
##  Max.   :8.000

hist(umf, xlab="distance (m)", main="", cex.lab=0.8, cex.axis=0.8)

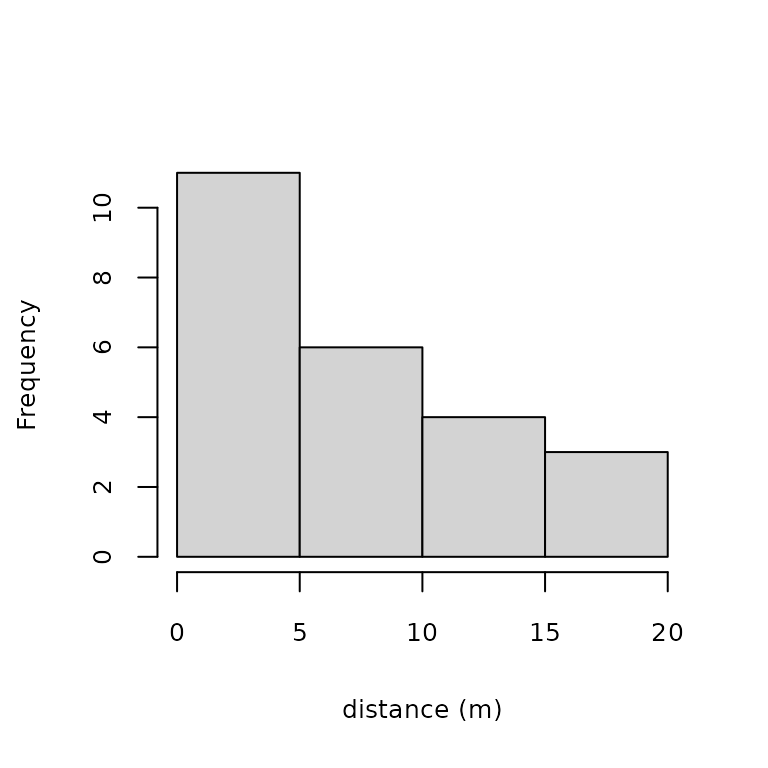
Figure 1. Histogram of detection distances

Model fitting

Now that we have put our data into an object of class unmarkedFrameDS, we are ready to fit some models with distsamp. The first argument is a formula which specifies the detection covariates followed by the density (or abundance) covariates. The only other required argument is the data, but several other optional arguments exist. By default, the half-normal detection function is used to model density in animals / ha. The detection function can be selected using the keyfun argument. The response can be changed from "density", to "abund" with the output argument. When modeling density, the output units can be changed from "ha" to "kmsq" using the unitsOut argument. distsamp also includes the arguments starts, method, and control, which are common to all unmarked fitting functions.

Below is a series of models that demonstrates distsamp’s arguments and defaults.

hn_Null <- distsamp(~1~1, umf)
hn_Null <- distsamp(~1~1, umf, keyfun="halfnorm", output="density",
    unitsOut="ha")
haz_Null <- distsamp(~1~1, umf, keyfun="hazard")
hn_Hab.Ht <- distsamp(~canopyHt ~habitat, umf)

The first two models are the same, a null half-normal detection function with density returned in animals / ha (on the log-scale). The third model uses the hazard-rate detection function, and the fourth model includes covariates affecting the Poisson mean (\(\lambda\)) and the half-normal scale parameter (\(\sigma\)).

Once a model has been fit, typing its name will display parameter estimate information and AIC. A summary method shows extra details including the scale on which parameters were estimated and convergence results.

haz_Null

## 
## Call:
## distsamp(formula = ~1 ~ 1, data = umf, keyfun = "hazard")
## 
## Density:
##  Estimate    SE    z P(>|z|)
##      2.97 0.959 3.09 0.00198
## 
## Detection:
##  Estimate   SE     z P(>|z|)
##      1.44 2.37 0.606   0.544
## 
## Hazard-rate(scale):
##  Estimate   SE       z P(>|z|)
##   -0.0223 1.21 -0.0185   0.985
## 
## AIC: 65.17091

Manipulating results

Back-transforming estimates to the original scale and obtaining standard errors via the delta method is easily accomplished:

names(haz_Null)

## [1] "state" "det"   "scale"

backTransform(haz_Null, type="state")

## Backtransformed linear combination(s) of Density estimate(s)
## 
##  Estimate   SE LinComb (Intercept)
##      19.4 18.6    2.97           1
## 
## Transformation: exp

backTransform(haz_Null, type="det")

## Backtransformed linear combination(s) of Detection estimate(s)
## 
##  Estimate   SE LinComb (Intercept)
##      4.21 9.99    1.44           1
## 
## Transformation: exp

backTransform(haz_Null, type="scale")

## Backtransformed linear combination(s) of Hazard-rate(scale) estimate(s)
## 
##  Estimate   SE LinComb scale
##     0.978 1.18 -0.0223     1
## 
## Transformation: exp

backTransform(linearComb(hn_Hab.Ht['det'], c(1, 5)))

## Backtransformed linear combination(s) of Detection estimate(s)
## 
##  Estimate   SE LinComb (Intercept) canopyHt
##      10.3 2.54    2.33           1        5
## 
## Transformation: exp

The first back-transformation returns population density, since this is the default state parameter modeled when distsamp’s output argument is set to "density". The second back-transformation returns the hazard-rate shape parameter, and third is the hazard-rate scale parameter. When covariates are present, backTransform in conjunction with linearComb should be used. Here, we requested the value of sigma when canopy height was 5 meters tall. Note that the intercept was included in the calculation by setting the first value in the linear equation to 1.

Parameters that do not occur in the likelihood may also be of interest. For example, the number of individuals occurring in the sampled plots (local population size) is a fundamental parameter in monitoring and conservation efforts. The following commands can be used to derive this parameter from our model of density:

site.level.density <- predict(hn_Hab.Ht, type="state")$Predicted
plotArea.inHectares <- 100 * 40 / 10000
site.level.abundance <- site.level.density * plotArea.inHectares
(N.hat <- sum(site.level.abundance))

## [1] 39.06128

To describe the uncertainty of N.hat, or any other derived parameter, we can use a parametric bootstrap approach. First we define a function to estimate N.hat, and then we apply this function to numerous models fit to data simulated from our original model.

getN.hat <- function(fit) {
    d <- predict(fit, type="state")$Predicted
    a <- d * (100 * 40 / 10000)
    N.hat <- c(N.hat = sum(a))
    return(N.hat)
    }
pb <- parboot(hn_Hab.Ht, statistic=getN.hat, nsim=25)
pb

## 
## Call: parboot(object = hn_Hab.Ht, statistic = getN.hat, nsim = 25)
## 
## Parametric Bootstrap Statistics:
##         t0 mean(t0 - t_B) StdDev(t0 - t_B) Pr(t_B > t0)
## N.hat 39.1          0.224             10.1          0.5
## 
## t_B quantiles:
##       0% 2.5% 25% 50% 75% 97.5% 100%
## N.hat 18   20  32  41  46    55   60
## 
## t0 = Original statistic computed from data
## t_B = Vector of bootstrap samples

Here, t_B is an approximation of the sampling distribution for N.hat, conditioned on our fitted model. Confidence intervals can be calculated from the quantiles of t_B. Note that in practice nsim should be set to a much larger value and a goodness-of-fit test should be performed before making inference from a fitted model. Parametric bootstrapping can be used for the latter by supplying a fit statistic such as SSE instead of getN.hat. See ?parboot and vignette('unmarked') for examples.

Prediction and plotting

A predict method exits for all unmarkedFit objects, which is useful when multiple covariate combinations exist. This method also facilitates plotting. Suppose we wanted model predictions from the covariate model along the range of covariate values studied. First we need to make new data.frames holding the desired covariate combinations. Note that column names must match those of the original data, and factor variables must contain the same levels.

head(habConstant <- data.frame(canopyHt = seq(2, 8, length=20),
    habitat=factor("A", levels=c("A", "B"))))

##   canopyHt habitat
## 1 2.000000       A
## 2 2.315789       A
## 3 2.631579       A
## 4 2.947368       A
## 5 3.263158       A
## 6 3.578947       A

(htConstant <- data.frame(canopyHt = 5,
    habitat=factor(c("A", "B"))))

##   canopyHt habitat
## 1        5       A
## 2        5       B

Now predict can be used to estimate density and \(\sigma\) for each row of our new data.frames.

(Elambda <- predict(hn_Hab.Ht, type="state", newdata=htConstant,
    appendData=TRUE))

##   Predicted       SE    lower    upper canopyHt habitat
## 1  16.22835 5.058481 8.809465 29.89506        5       A
## 2  10.91326 4.370499 4.978158 23.92436        5       B

head(Esigma <- predict(hn_Hab.Ht, type="det", newdata=habConstant,
    appendData=TRUE))

##   Predicted       SE    lower    upper canopyHt habitat
## 1  10.76998 4.259542 4.960935 23.38117 2.000000       A
## 2  10.72259 3.968438 5.191220 22.14777 2.315789       A
## 3  10.67541 3.693948 5.418117 21.03394 2.631579       A
## 4  10.62844 3.439012 5.637007 20.03965 2.947368       A
## 5  10.58167 3.207199 5.842026 19.16659 3.263158       A
## 6  10.53511 3.002718 6.026005 18.41826 3.578947       A

Once predictions have been made, plotting is straight-forward. Figure 2a shows density as a function of habitat type, and Figure 2b shows that \(\sigma\) is not related to canopy height.

par(mfrow=c(1, 2))
with(Elambda, {
    x <- barplot(Predicted, names=habitat, xlab="Habitat",
        ylab="Density (animals / ha)", ylim=c(0, 25), cex.names=0.7,
        cex.lab=0.7, cex.axis=0.7)
    arrows(x, Predicted, x, Predicted+SE, code=3, angle=90, length=0.05)
    box()
    })
with(Esigma, {
    plot(canopyHt, Predicted, type="l", xlab="Canopy height",
        ylab=expression(paste("Half-normal scale parameter (", sigma, ")",
        sep="")), ylim=c(0, 20), cex=0.7, cex.lab=0.7,
    cex.axis=0.7)
    lines(canopyHt, Predicted+SE, lty=2)
    lines(canopyHt, Predicted-SE, lty=2)
    })

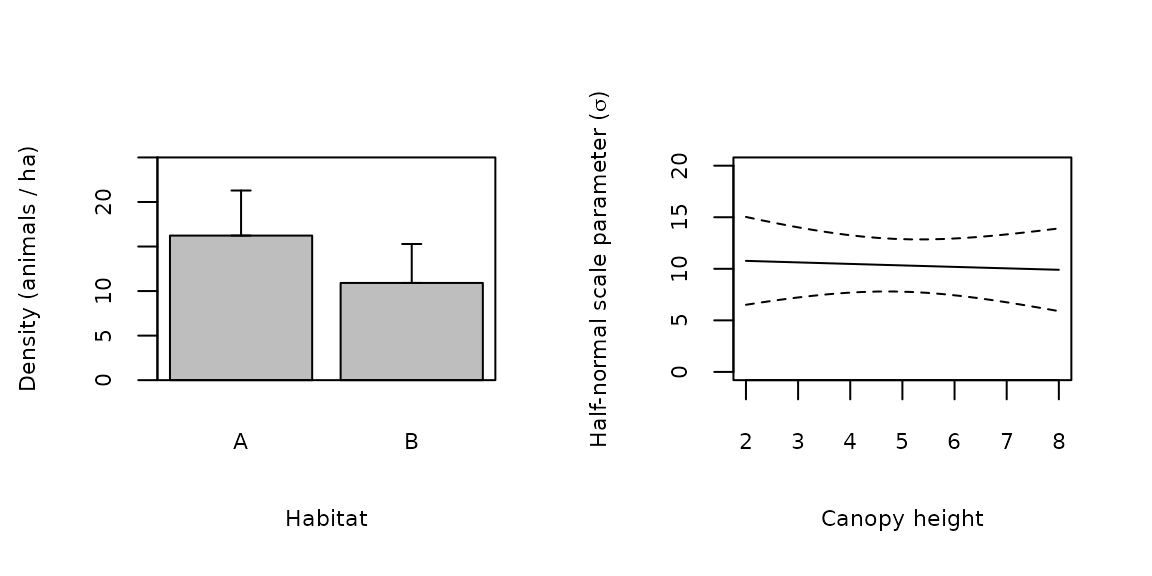
Figure 2. Predicted covariate relationships

Plots of the detection function parameters can be less informative than plots of the detection functions themselves. To do the latter, we can plug predicted values of \(\sigma\) at given covariate values into the gxhn function. For instance, Figure 3a shows to the half-normal function at a canopy height of 2m. This was plotted by setting \(\sigma\) to 10.8, the predicted value shown above. The available detection functions are described on the detFuns help page. Probability density functions such as dxhn can be plotted with the distance histogram using the hist method for unmarkedFitDS objects (Figure 3b). This only works for models without detection covariates; however, probability density functions at specific covariate values can be added in a fashion similar to that above (Figure 3b).

par(mfrow=c(1, 2))
plot(function(x) gxhn(x, sigma=10.8), 0, 20, xlab="Distance (m)",
    ylab="Detection prob. at 2m canopy ht.", cex.lab=0.7,
    cex.axis=0.7, las=1)
hist(hn_Null, xlab="Distance (m)", ylab="Probability density", main="",
    ylim=c(0, 0.1), cex.lab=0.7, cex.axis=0.7, las=1)
plot(function(x) dxhn(x, sigma=10.8), 0, 20, add=TRUE, col="blue")
plot(function(x) dxhn(x, sigma=9.9), 0, 20, add=TRUE, col="green")
legend('topright', c("Canopy ht. = 2m", "Null", "Canopy ht. = 8m"),
    col=c("blue", "black", "green"), lty=1, cex=0.4)

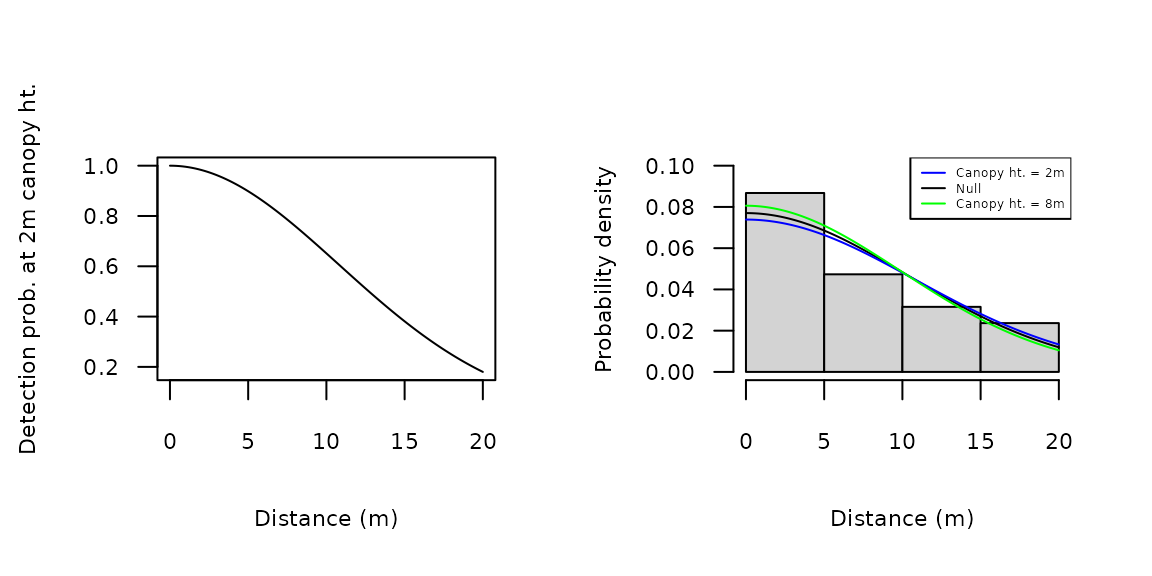
Figure 3. Detection and probability density functions

Model extensions

A common criticism of distance sampling is that all individuals must be available for detection. Similarly, the probability of detecting an individual a distance of 0 must be 1. These assumptions often cannot be met. For instance, when counting cues such as bird songs or whale blows, the probability that an individual will produce a cue (and thus be available for detection) is rarely 1 during the sampling interval. Recently developed methods (Chandler et al. 2011) allow for the estimation of the probability of being available for detection \(\phi\). To do so, replicate distance sampling observations must be collected at each transect. These replicates could be collected using repeated visits or multiple observers working independently. Implementation of this model in unmarked is accomplished using the gdistsamp function. The function also provides the option to model abundance using the negative binomial distribution. Formatting data and specifying models is similar to methods described above and is more fully outlined in the help pages.

Conclusion

This document has emphasized methods tailored to distance sampling analysis; however, the more general methods available in package unmarked can also be applied to models fitted using distsamp and gdistsamp. For example, model-selection and model-averaging can be accomplished using the fitList function and the modSel and predict methods.

References

Buckland, S. T., D. R. Anderson, K. P. Burnham, J. L. Laake, D. L. Borchers, and L. Thomas. 2001. Introduction to distance sampling – estimating abundance of biological populations. Oxford University Press.

Chandler, R. B., J. A. Royle, and D. I. King. 2011. Inference about density and temporary emigration in unmarked populations. Ecology 92:1429–1435.

Royle, J. A., D. K. Dawson, and S. Bates. 2004. Modeling abundance effects in distance sampling. Ecology 85:1591–1597.